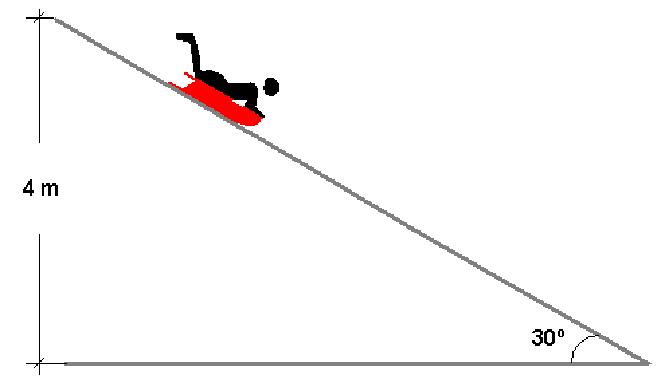
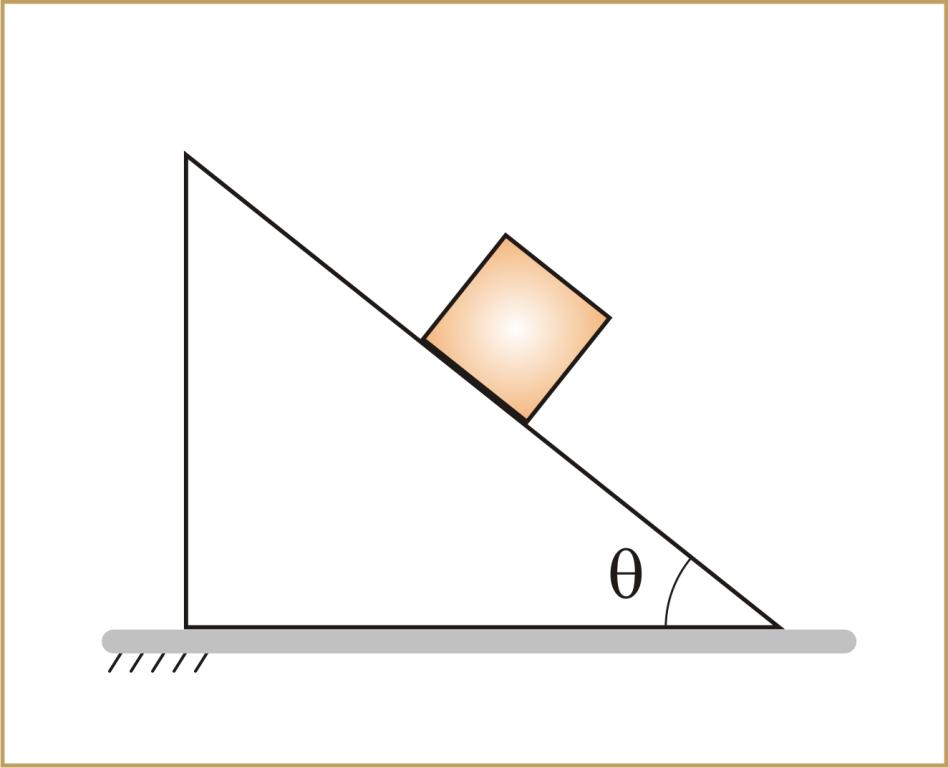
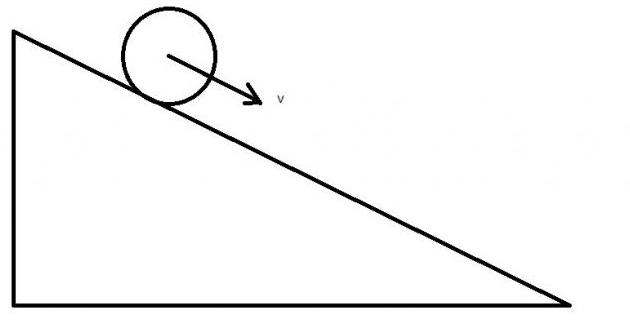
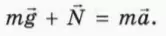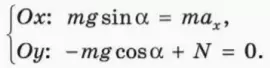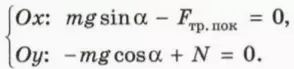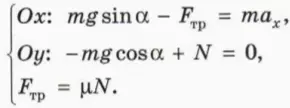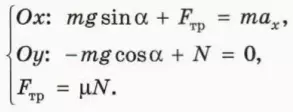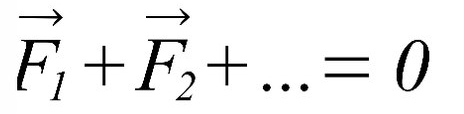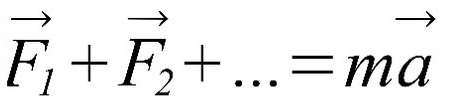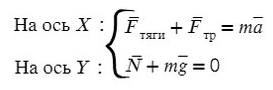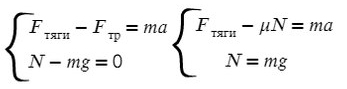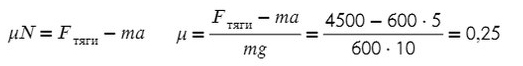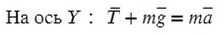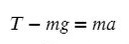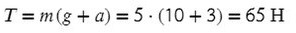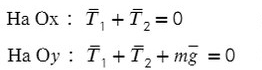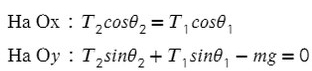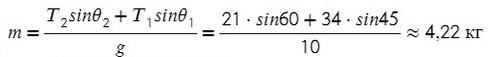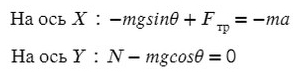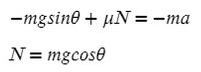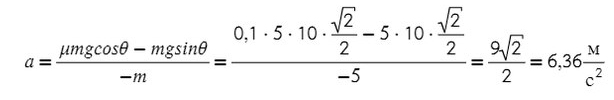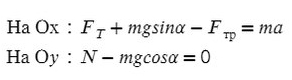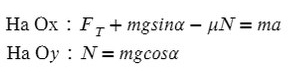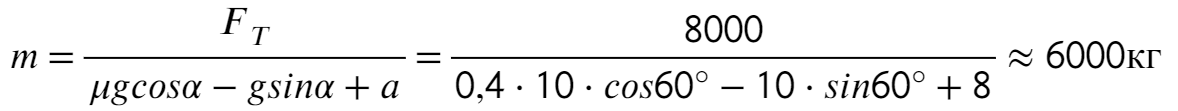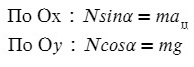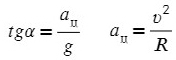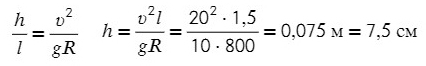День бруска на наклонной плоскости праздник

1. Тело на гладкой наклонной плоскости

Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.

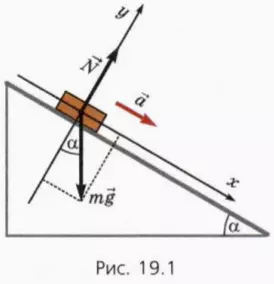
На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m и сила нормальной реакции (рис. 19.1).

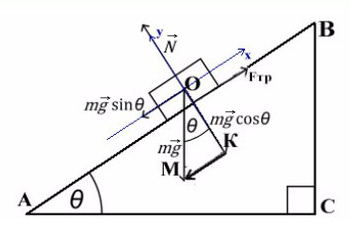
Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.

Уравнение второго закона Ньютона в векторной форме имеет вид

? 1. Объясните, почему справедливы следующие уравнения:

? 2. Чему равна проекция ускорения тела на ось x?

? 3. Чему равен модуль силы нормальной реакции?

? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?

? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?

При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.

? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v₀.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?

? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?

2. Условие покоя тела на наклонной плоскости

Будем теперь учитывать силу трения между телом и наклонной плоскостью.

Если тело покоится на наклонной плоскости, на него действуют сила тяжести m, сила нормальной реакции и сила трения покоя _тр.пок (рис. 19.2).

Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска. Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:

F_{тр.пок x} = –F_тр.пок

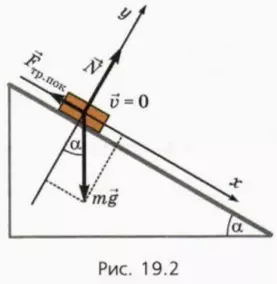
? 8. Объясните, почему справедливы следующие уравнения:

? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?

? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством

μ ≥ tgα.

Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству F_тр.пок ≤ μN.

Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).

? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?

? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?

Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!

? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:
а) вниз? б) вверх?

3. Движение тела по наклонной плоскости с учетом трения

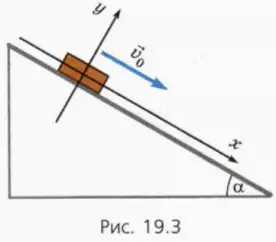
Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.

? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 16. Чему равна проекция ускорения тела на ось x?

? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?

? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?

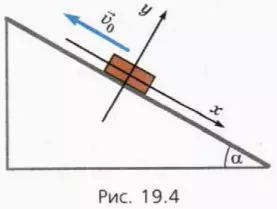
Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).

? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 20. Чему равна проекция ускорения тела на ось x?

? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?

? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v₀. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?
б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?

? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?

Зацените!! Езда Электро-Велосипеда по воде

Дополнительные вопросы и задания

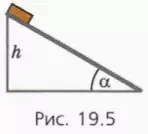
24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?

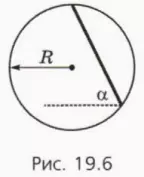
25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.

26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?

27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см. Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?

28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?
в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.

Источник

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r — радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

тяжести;
реакции опоры;
трения качения и/или скольжения;
натяжение нити;
сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) — F_r= m*a

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) — µ*cos(φ)) = m*a =>

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) — F_r= m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) — 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Источник

Проецирование сил. Движение по наклонной плоскости

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Неколлинеарные силы.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

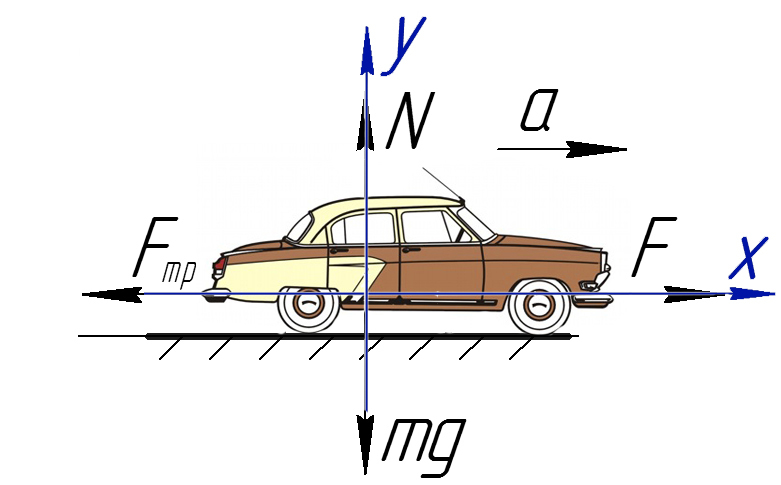
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Получаем, что:

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Ответ: 0,25

Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

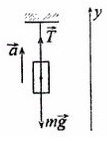
Сделаем рисунок, покажем силы, которые дествуют на груз

T — сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Ответ: 65 Н

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

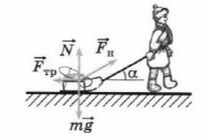
Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

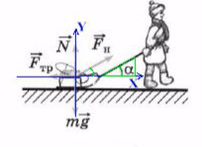
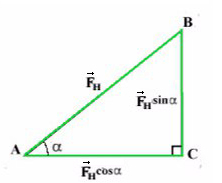
Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

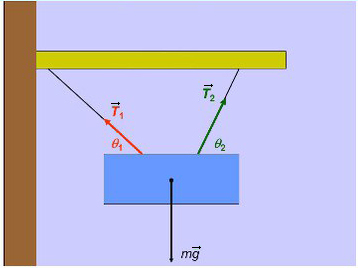
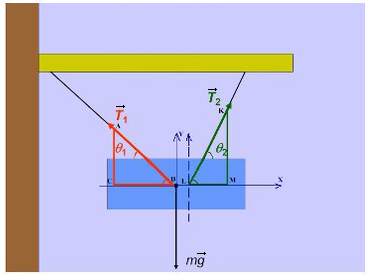
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

Ответ: 4,22 кг

Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
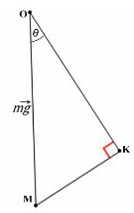
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

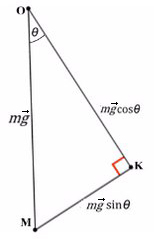
Рассмотрим поподробнее ΔKOM:

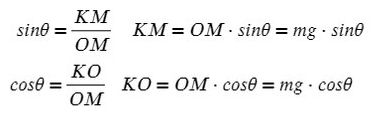
Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Ответ: 6,36 м/с²

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

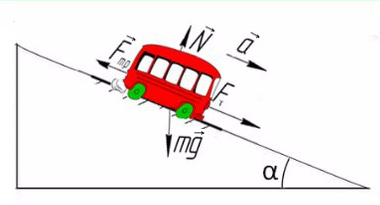
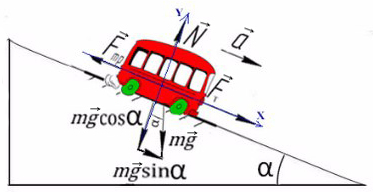
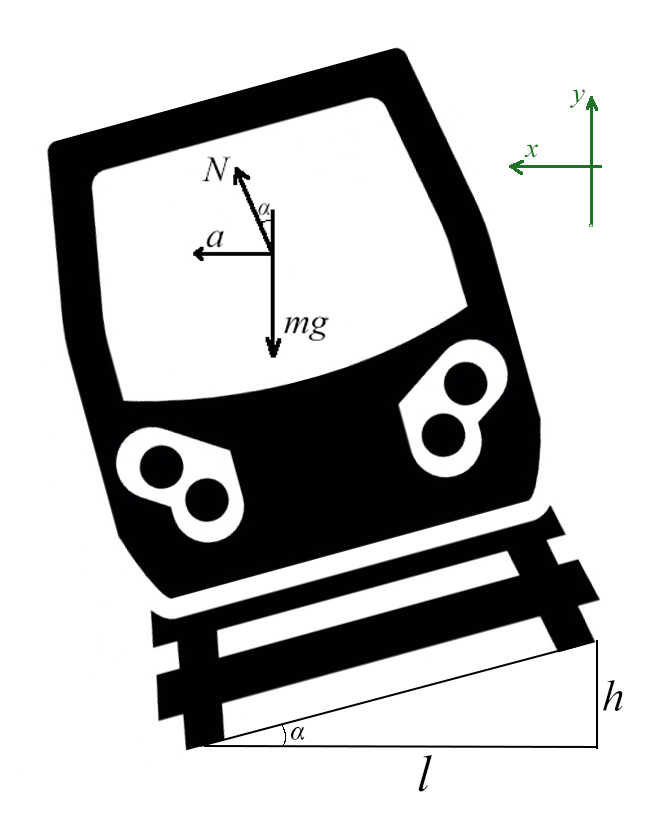
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Ответ: 6000 кг

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное — понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс — это отношение противолежащего катета к прилежащему:

Ответ: 7,5 см

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Будь в курсе новых статеек, видео и легкого технического юмора.

Источник

§4. Примеры из физики

Простейшие примеры векторов в физике — скорость и сила.

1. Всякое движение можно представить как результат сложения нескольких движений, его составляющих. Скорость результирующего движения изображается по величине и направлению диагональю параллелограмма, построенного на отрезках, изображающих составляющие скорости, как на сторонах. Рассмотрим конкретный пример.

Рыбак переправляется на лодке `A` через реку, которая течёт в сторону, указанную стрелкой (рис. 18). Пусть скорость течения воды `vec(v_1)` изображается по величине и направлению отрезком `AB`, а скорость `vec(v_2)` движения лодки относительно воды под влиянием усилий гребца изображается отрезком `AC` (в стоячей воде лодка двигалась бы по направлению `AC` со скоростью `vec(v_2)`). Лодка будет двигаться относительно берега по направлению `AM` со скоростью `vec v`, изображаемой диагональю `AD` параллелограмма, построенного на векторах `vec(v_1)` и `vec(v_2)` (в данном случае параллелограмм `ABCD` является прямоугольником).

2. Сила — как векторная величина — всегда имеет определённое направление, модуль, а также точку приложения.

Часто встречаются случаи, когда на тело действуют несколько сил. Тогда бывает удобно заменить их одной силой, которая производит на тело такое же действие, как и несколько одновременно действующих сил. Такую силу (если она существует) называют равнодействующей. Нахождение равнодействующей нескольких сил осуществляется с помощью правил векторного сложения, при этом слагаемые силы называют составляющими.

Так, несколько сил, действующих на одну и ту же точку тела, всегда можно заменить одной равнодействующей, как бы ни были направлены силы и каковы бы ни были их величины. Пусть, например, на тело действуют четыре силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и `vec(F_4)`, приложенные к одной точке `O` и лежащие в одной плоскости (рис. 19). Тогда их равнодействующая `vec F` будет равна векторной сумме этих сил, найденной по правилу многоугольника (рис. 20).

Найти равнодействующую `vec R` трёх равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми силами равны между собой.

`F_1 = F_2 = F_3 = F`.

См. рис. 21. Углы между парами векторов `vec(F_1)` и `vec(F_2)`, `vec(F_2)` и `vec(F_3)`, а также между векторами `vec(F_1)` и `vec(F_3)`, равны друг другу и равны `120^@`. Сложим силы `vec(F_2)` и `vec(F_3)` по правилу параллелограмма. Вследствие равенства модулей сил `vec(F_2)` и `vec(F_3)` этот параллелограмм есть ромб. Сумма сил `vec(F_2) + vec(F_3)` есть диагональ ромба, поэтому углы между парами векторов `vec(F_2)` и `vec(F_2) + vec(F_3)`, а также `vec(F_3)` и `vec(F_2) + vec(F_3)` равны по `60^@`, т. е. векторы `vec(F_1)` и `vec(F_2) + vec(F_3)` направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах `vec(F_2)` и `vec(F_3)`, состоит из двух равносторонних треугольников, поэтому модуль силы

`|vec(F_2) + vec(F_3)| = F_2 = F_3 = F = F_1`, т. е `vec F_1 = — (vec(F_2) + vec(F_3))`,

откуда следует `vec(F_1) + vec(F_2) + vec(F_3) = 0`.

К телу приложено `6` сил, лежащих в одной плоскости и составляющих друг с другом углы в `60^@`. Силы последовательно равны `1`, `2`, `3`, `4`, `5` и `6 Н`. Найти равнодействующую `vec R` этих шести сил.

Сложение сил по правилу многоугольника здесь нецелесообразно. Поступим иначе. Сложим сначала попарно силы, направленные вдоль одной прямой (см. рис. 22 а, б, в).

Получим

`|vec(F_2) + vec(F_4)| = 4 — 1 = 3`,

аналогично `|vec(F_2) + vec(F_5)| = 5 — 2 = 3` и `|vec(F_3) + vec(F_6)| = 6 — 3 = 3`.

Сумма сил `vec(F_2) + vec(F_5)` направлена вдоль вектора `vec(F_5)`. Туда же направлена и сумма сил `vec(F_1) + vec(F_4) + vec(F_3) + vec(F_6)`, причём модуль этой силы равен `3`. В итоге получаем, что сумма всех шести сил `vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)` направлена вдоль направления силы `vec(F_5)`, а модуль этой силы `|vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)| = 3 + 3 = 6 Н`.

Найти равнодействующую `vec R` пяти равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой (см. рис. 23). (Эти углы, разумеется, равны `360^@ //5 = 72^@`.)

В отличие от предыдущего примера здесь мы имеем нечётное число сил, поэтому невозможно образовать из них целое число пар. Поступим иначе. Возьмём какую-нибудь силу, например, `vec(F_1)`, а остальные сгруппируем в пары и попарно сложим их (см. рис. 24):

`vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`.

Почему удобна именно такая группировка сил в пары? Дело в том, что обе суммы сил (и `vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`) направлены вдоль линии действия силы `vec(F_1)`. Ясно, что равнодействующая всех сил будет направлена вдоль линии действия силы `vec(F_1)`. Модули сумм сил легко найти из геометрии. Например, в силовом параллелограмме, построенном на векторах `vec(F_2)` и `vec(F_5)`, который является ромбом, длина диагонали ромба (модуль силы `vec(F_2) + vec(F_5)`) равна удвоенной половинке диагонали, а та легко ищется из любого из четырёх прямоугольных треугольников, на которые ромб разбивается диагоналями. В результате

`|vec(F_2) + vec(F_5) | = 2F cos 72^@`,

где `F` — модуль любой из пяти исходных сил. Аналогично

`|vec(F_3) + vec(F_4)| = 2F cos 36^@`.

В итоге для модуля искомой силы получаем формулу

`R = F(1 + 2 cos 72^@ — 2 cos 36^@)` (*).

Для углов `72^@` и `36^@` нет таких простых формул, как для углов `30^@`, `45^@` или `60^@`. Пользуясь калькулятором, можно, однако, показать, что согласно формуле (*) `R = 0`.

Имеется и более красивое доказательство того, что результирующий вектор есть нулевой вектор. В самом деле, мы довольно произвольно взяли в качестве силы, которой не хватило пары, силу `vec(F_1)`. Если бы в качестве такой взять силу `vec(F_2)`, а в пары объединить `vec(F_1)` и `vec(F_3)` (одна пара) и `vec(F_4)` и `vec(F_5)`, то, повторив рассуждения, получим, что равнодействующая всех пяти сил `vec R` должна быть направлена вдоль линии действия силы `vec(F_2)`. Возможно ли, чтобы вектор был одновременно направлен вдоль двух несовпадающих друг с другом направлений (и `vec(F_1)`, и `vec(F_2)`; а на самом деле, как догадался читатель, ещё и вдоль направления действия сил `vec(F_3)`, `vec(F_4)` и `vec(F_5)`!)? Ненулевым вектор не может быть! Остаётся одна возможность: суммарный вектор – нулевой!

В примерах 10 и 11 мы искали по правилу параллелограмма суммы сил.

В примере 12 нас интересовала лишь проекция равнодействующей силы на направление (например, силы `vec(F_1)`).

В следующих примерах наш интерес будет также скорее не к равнодействующей силе, а только к каким-то её проекциям.

Электрический фонарь весом `Q = 16 Н` укреплён, как показано на рис. 25.

Определите отношение натяжений `T_1` и `T_2` в проволоках `BA` и `BC`, углы наклона которых даны на рисунке.

В условиях равновесия сумма всех сил, приложенных к точке `B`, равна нулю. Поэтому проекция равнодействующей всех сил на горизонтальное направление тоже равна нулю. Проекция силы со стороны проволоки, идущей к фонарю, на это направление равна нулю (эта сила вертикальна). Остаются вклады от двух натяжений со стороны проволок `BA` и `BC`. Горизонтальную ось направим слева направо. Тогда имеем: T1, гор+T2, гор=0T_{1,;mathrm{гор}}+T_{2,;mathrm{гор}}=0 (см. рис. 26), т. е.

`T_1 * cos 60^@ — T_2 cos 45^@ = 0`

(или `T_1 * sin 30^@ — T_2 sin 45^@ = 0`), откуда получаем `T_1//T_2 = sqrt2`.

Однородная массивная верёвка подвешена за два конца на разных высотах (см. рис. 27). Масса верёвки `m`. Углы, которые составляет верёвка с вертикалью в точках закрепления, равны `30^@` и `60^@`.

Определите силы натяжения верёвки вблизи её точек крепления.

Задача кажется очень трудной, т. к. не ясно, какую роль играет неизвестная нам форма верёвки, которую она примет под действием сил тяжести всех частей верёвки. (В предыдущем примере мы не интересовались провисанием проволок под действием силы тяжести, молчаливо считая провисание малым.) И всё же задача в той постановке, в какой дана, имеет простое решение. Мысленно проведём горизонтальную ось слева направо. Поскольку верёвка находится в равновесии, то сумма проекций всех сил на горизонтальное направление равна нулю. Сила тяжести верёвки имеет нулевую проекцию на это направление (эта сила направлена вертикально). Снова остаются вклады от двух натяжений (см. рис. 28):

T1, гор+T2, гор=0T_{1,;mathrm{гор}}+T_{2,;mathrm{гор}}=0, или `- T_1 * sin 30^@ + T_2 sin 60^@ = 0`.

Полагая `sin 30^@ = 1//2` и `sin 60^@ = sqrt3 //2`, находим `T_1 // T_2 = sqrt3`. Мысленно проведём ещё и вертикальную ось, направив её вниз. Сумма проекций всех сил на эту ось также равна нулю:

`mg — T_1 cos 30^@ — T_2 cos 60^@ = 0`.

Учитывая найденное ранее соотношение между `T_1` и `T_2` и значения `cos 60^@ = 1//2` и `cos 30^@ = sqrt3 //2`, получаем:

`mg — sqrt3 * T_2 * sqrt3 //2 — T_2 //2 = 0`,

откуда

`T_2 = mg//2` и `T_1 = sqrt3 mg//2`.

На гладкой наклонной плоскости с углом наклона `alpha` лежит брусок массой `m`. Какую горизонтальную силу нужно приложить к бруску, чтобы он находился в покое (рис. 29)?

Определите также модуль нормальной силы реакции на брусок со стороны наклонной плоскости.

Брусок по условию задачи покоится. Значит, сумма всех сил, приложенных к бруску, равна нулю. Равны нулю и суммы проекций сил на любые направления, в частности, на направление вдоль наклонной плоскости и перпендикулярное ему. Нормальная сила реакции `vec N` со стороны наклонной плоскости имеет равную нулю составляющую вдоль наклонной плоскости.

Проекция сила тяжести `m vec g` на ось `Ox` вдоль наклонной плоскости (рис. 30) равна `- mg sin alpha`, а проекция горизонтальной силы `F` на эту ось равна `F cos alpha`. Других сил вдоль наклонной плоскости не действует (плоскость, по условию задачи, гладкая, т. е. сила трения пренебрежимо мала). Приравнивая нулю сумму проекций на ось `Ox` всех сил, действующих на тело, получаем: `- mg sin alpha + F cos alpha = 0`, откуда находим

`F = mg (sin alpha)/(cos alpha) = mg * bbb»tg» alpha`.

Для отыскания `N` обратимся к проекциям сил на направление `Oy`. Приравняем нулю и сумму проекций на ось `Oy`:

`N — mg cos alpha — F sin alpha = 0`,

откуда `N = mg cos alpha + F sin alpha`, или с учётом найденного значения `F`:

`N = mg cos alpha + mg (sin^2 alpha)/(cos alpha) = mg (cos^2 alpha + sin^2 alpha)/(cos alpha)`,

тогда с учётом основного тригонометрического тождества, `sin^2 alpha + cos^2 alpha = 1`, получаем окончательно

`N = (mg)/(cos alpha)`.

На шероховатой поверхности доски лежит брусок массой `m`. К нему приложена сила, направленная под углом `alpha` к горизонту (см. рис. 31).

Определите модуль нормальной силы реакции со стороны поверхности.

Поскольку брусок не проваливается и не подскакивает вверх, то сумма проекций сил на вертикальную ось равна нулю:

`N + F * sin alpha — mg = 0`,

(см. рис. 32), откуда находим

`N = mg — F * sin alpha`.

Часто совершенно безосновательно приравнивают силу реакции `N` силе тяжести `mg`. Мы видим, что даже в случае горизонтальной поверхности это в общем случае не так. Для наклонной плоскости это тоже не так. В предыдущем примере нормальная сила реакции равнялась `mg//cos alpha`. Кстати, если бы удерживающая сила `F` действовала там не вдоль горизонтали, а вдоль наклонной плоскости, то для удержания бруска на наклонной плоскости потребовалась бы сила величиной `F = mg sin alpha`, а нормальная сила реакции была бы равна `N = mg cos alpha` (и снова не равнялась бы `mg`!)

Докажите это самостоятельно.

Самолёт взлетает с аэродрома со скоростью v=220 км/чv=220;mathrm{км}/mathrm ч под углом `alpha = 20^@` к горизонту. Найдите модули горизонтальной и вертикальной составляющих скорости самолёта.

(См. рис. 33). В данном примере мы имеем дело с весьма простым случаем разложения скорости на два взаимно перпендикулярных направления:

`vec v = vec(v _sf»гор») + vec(v_sf»верт»)`,

vгор=v cos α≈207 км/чv_mathrm{гор}=v;cos;alphaapprox207;mathrm{км}/mathrm ч, vверт=v sin α≈75 км/чv_mathrm{верт}=v;sin;alphaapprox75;mathrm{км}/mathrm ч.

В безветренную погоду самолёт летит на север со скоростью 180 км/ч180;mathrm{км}/mathrm ч (50 м/с50;mathrm м/mathrm с) относительно земли. С какой скоростью относительно земли будет лететь самолёт, если дует западный ветер со скоростью 10 м/с10;mathrm м/mathrm с?

(См. рис. 34). В данном случае мы имеем дело со сложением движений: `vec(v_sf»с») = vec(v_sf»св») + vec(v_sf»в»)`, где `vec(v_sf»св»)` — скорость самолёта относительно воздуха (модуль которой равен скорости самолёта относительно земли в безветренную погоду), а `vec(v_sf»в»)` — скорость воздуха. Далее по теореме Пифагора получаем:

vс=502+102=2600≈51 м/сv_mathrm с=sqrt{50^2+10^2}=sqrt{2600}approx51;mathrm м/mathrm с.

Лодка пытается пересечь реку, текущую со скоростью u=3 км/чu=3;mathrm{км}/mathrm ч. Скорость лодки в стоячей воде v=5 км/чv=5;mathrm{км}/mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить лодку, чтобы она двигалась поперек реки (без сноса)? Какой будет при этом модуль скорости лодки `v` относительно берега?

Как и в примере 9, мы также имеем дело со случаем сложения движений. Но там было проще: не требовалось выбирать никакой стратегии, рыбак лишь наблюдал, как снесёт его лодку течением воды в реке. Если бы вода в реке покоилась, то, направив корпус лодки под углом `alpha` к нормали, мы заставили бы её двигаться в направлении вектора `vec V` (см. рис. 35). В действительности, вода в реке не стоячая, а имеет скорость `vec u` Поэтому сносимая течением лодка будет двигаться в направлении вектора `vec v` таком, что `vec v = vec V + vec u`. Учитывая, что оба треугольника в параллелограмме на рис. 35 прямоугольные (по условию, лодка должна двигаться перпендикулярно берегам), находим

`sin alpha = u//V = 3//5`, `alpha ~~ 37^@`,

а по теореме Пифагора v=V2-u2=4 м/сv=sqrt{V^2-u^2}=4;mathrm м/mathrm с.

Лодка пытается пересечь реку, текущую со скоростью u=5 км/чu=5;mathrm{км}/mathrm ч. Скорость лодки в стоячей воде V=3 км/чV=3;mathrm{км}/mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить корпус лодки, чтобы её снесло как можно меньше? Под каким углом `beta` к нормали к берегу будет при этом плыть лодка?

В данном примере скорость лодки относительно воды меньше, чем скорость воды в реке, `V < u`, поэтому реализовать план из предыдущего примера (рис. 35) невозможно. Наша цель состоит в том, чтобы направить корпус лодки под таким углом `alpha` к нормали к берегу, чтобы сносимая течением лодка двигалась под углом `beta`, по возможности наименьшим (см. рис. 36 ф, б, в).

В данном примере складывать скорости (лодки относительно воды `vec V` и воды в реке `vec u`) удобно по правилу треугольника, а не параллелограмма: приставим начало вектора `vec V` к концу вектора `vec u`. Выбирая оптимальный план (с наименьшим углом сноса), будем мысленно поворачивать вектор `vec V`. При этом конец вектора будет описывать окружность с центром в конце вектора `vec u`. Из рисунков видно, что минимальному углу сноса лодки `beta` соответствует случай, когда вектор `vec v = vec V + vec u` направлен по касательной к этой окружности. При этом вектор `vec V _|_ vec v` т. е. треугольник скоростей на рис. 36 в прямоугольный. Отсюда получаем:

`sin alpha = V//u = 3//5`; `alpha ~~37^@`; `beta = 90^@ — alpha ~~53^@`.

Лодку вытягивают из воды, стоя на крутом берегу и выбирая верёвку, которая привязана к носу лодки, со скоростью `v` (см. рис. 37).

Какой будет скорость лодки `u` в момент, когда верёвка будет составлять угол `alpha` с горизонтом? Верёвка нерастяжима.

Традиционная ошибка решающих эту задачу состоит в том, что пытаются разложить движение лодки на два направления – горизонтальное и вертикальное, делая (неправильное!) построение, как показано на рис. 38а и получая неверный ответ `u = v * cos alpha`. Что здесь неправильно? В отличие от самолёта из примера 17, который двигался под отличным от нуля углом к горизонту (см. рис. 33), здесь лодка движется горизонтально! Сделаем другое разложение скорости лодки `vec u` по двум направлениям – вдоль верёвки (в данный момент времени!) и перпендикулярно ей (см. рис. 38б).

Проекция вектора `vec u` на направление верёвки будет равна скорости `v`, с которой выбирают верёвку: `v = u cos alpha`, поэтому `u = v/(cos alpha)`.

Поясним ещё, почему проекция вектора `vec u` на направление верёвки будет равна скорости `v` с которой выбирают верёвку. Если мы имеем абсолютно твердое тело (АТТ), деформациями в котором можно пренебречь, или нерастяжимую нить (но уже максимально натянутую), то как бы ни двигались АТТ или нерастяжимая нить, они будут обладать следующим свойством. Возьмём две произвольные точки `A` и `B` нити или АТТ и мысленно соединим их прямой. Тогда составляющие скоростей выбранных точек вдоль этой прямой в любой момент времени будут равны друг другу: vA∥→=vB∥→overrightarrow{v_{Aparallel}}=overrightarrow{v_{Bparallel}} (см. рис. 39). В противном случае изменялось бы расстояние между точками `A` и `B`. Составляющие скорости, перпендикулярные отрезку прямой `AB`, могут быть при этом любыми.

Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 40). В некоторый момент времени силы натяжения тросов, идущих от лодок 1 и 2, равны друг другу по модулю и равны `F`. Угол между тросами равен `2 alpha`. Какая равнодействующая сила приложена к буксируемой лодке со стороны тянущих её лодок? Чему будет равна эта сила в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?

Две силы нужно сложить по правилу параллелограмма, который в данном случае будет ещё и ромбом с перпендикулярными друг другу диагоналями, разбивающими его на четыре равных прямоугольных треугольника. Из геометрии рис. 41 видно, что модуль равнодействующей силы `R` равен удвоенной длине прилежащего катета: `R = 2F cos alpha`. При стремлении угла между направлениями тросов к нулю `R -> 2F` (`cos alpha -> 1` при `alpha -> 0`).

Хитрее оказывается похожая задача, когда заданы не силы, а скорости.

Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 42). В некоторый момент времени модули скоростей лодок 1 и 2 равны друг другу и равны `v_1 = v_2 = v`. Найти модуль и направление скорости буксируемой лодки `u`. Тросы нерастяжимы. Чему будет равна эта скорость в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?

Ясно, что «решение» `u = 2v cos alpha` (как в предыдущем примере) не подходит, т. к. при `alpha -> 0` мы получили бы, что `u -> 2v`, чего не может быть. Если, например, две собаки в упряжке бегут с одинаковыми скоростями `v` в одном направлении, то и скорость упряжки будет равна этой же скорости `v` (если, конечно, упряжка не отцепилась или к ней не подключили дополнительно мотор).

Решение задачи такое же, как в примере 21. В данном примере важнейшими словами являются «Тросы нерастяжимы». Ясно, что правильное построение, учитывающее это условие, должно быть таким, как на рис. 43, откуда немедленно получаем `v = u cos alpha`, поэтому `u = v/(cos alpha)`. Тогда в предельном случае, когда `alpha -> 0`, имеем `u -> v`, как и должно быть.

Заметим, что четырёхугольник на рис. 43 весьма мало похож на параллелограмм из предыдущего примера. Еще меньше будет похож на параллелограмм этот четырёхугольник, когда модули скоростей `v_1 != v_2` (см. рис. 44).

Две лодки буксируют третью с помощью двух тросов (рис. 45). В некоторый момент времени скорость 2-ой лодки в 2 раза больше, чем скорость 1-ой, `v_2 = 2v_1 = 2v`, а угол между тросами равен `90^@`. В каком направлении и с какой скоростью движется в этот момент буксируемая лодка? Тросы нерастяжимы.

В данном случае четырёхугольник на рис. 44 будет прямоугольником — см. рис. 46 (т. е. всё же параллелограммом).

По определению тангенса угла `»tg»varphi _1 = v_2 //v_1 = 2`, откуда, пользуясь калькулятором, находим `varphi _1 ~~63^@`; `varphi _2 = 90^@ — varphi _1 ~~ 27^@`.

Модуль скорости буксируемой лодки найдём по теореме Пифагора (раз уж у нас «случайно» появились прямоугольные треугольники):

`u = sqrt(v_1^2 + v_2^2) = sqrt(v^2 + (2v)^2) = sqrt5 * v ~~ 2,2 v`.

Источник

Брусок массой 2 кг находится на наклонной плоскости с углом наклона 30. Какую силу, направленную параллельно плоскости,

Чтобы найти значение приложенной к указанному бруску силы, спроецируем действующие силы на поверхность наклонной плоскости: m * a = 0 (брусок должен находиться в покое) = F — Fт * sinα = F — m * g * sinα, откуда выразим: F = m * g * sinα.

Постоянные и переменные: m — масса бруска (m = 2 кг); g — ускорение свободного падения (g ≈ 10 м/с 2 ); α — наклон плоскости (α = 30º).

Помогите решить задачу по физике

С какой горизонтальной силой надо действовать на брусок массой 2 кг , находящийся на наклонной плоскости с углом наклона 30 градусов,чтобы он двигался равномерно вверх по наклонной плоскости? Коэффициент трения бруска о наклонную плоскость равен 0,3

Дано: m=2кг; угол 30 градусов; мю=0,3
F-?

Ответ: сила F должна быть 21,222 Н

Тренировочный вариант ЕГЭ №210222 по физике с ответами 100 баллов

Тренировочный вариант решу ЕГЭ 2021-2022 по физике КИМ №210222 (№13) для 11 класса с ответами и решением для подготовки к экзамену на 100 баллов от 22.02.2021 (22 февраля 2021 года), вариант составлен по новой демоверсии ФИПИ.

Ссылка для скачивания пробного ЕГЭ: задания и ответы

Ответы и решения для заданий опубликованы в конце варианта.

Решу ЕГЭ по физике тренировочный вариант №210222 с ответами онлайн:

Ответы и задания из варианта:

1)На рисунке показан график зависимости проекции скорости vх от времени t. Определите проекцию перемещения тела за первые 3 с?

ответ: 0

2)К системе из кубика массой М = 1 кг и двух пружин приложена постоянная горизонтальная сила F величиной 9 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жесткость первой пружины k1 = 300 Н/м. Жесткость второй пружины k2 = 600 Н/м. Каково удлинение первой пружины? Ответ дать в сантиметрах.

ответ: 3

3)Два тела движутся с одинаковой скоростью. Кинетическая энергия первого тела в 4 раза меньше кинетической энергии второго тела. Определите отношение m1/m2 масс тел.

ответ: 0,25

4)На рисунке изображены силы, действующие на шест, прислонённый к стене. Каково плечо силы F относительно оси, проходящей через точку O (середина шеста) перпендикулярно плоскости рисунка? Расстояния от угла стены до точек касания шестом стены АВ = 0,8 м, ВС = 0,6 м.

ответ: 0

5)На наклонной плоскости находится брусок массой 2 кг, для которого составили таблицу зависимости модуля силы трения Fтр от угла наклона плоскости к горизонту α с погрешностью не более 0,01 Н. Основываясь на данных, приведённых в таблице, и используя закон сухого трения, выберите два верных утверждения.

1) Сила трения скольжения не зависит от угла наклона плоскости.
2) При увеличении угла наклона от 0 до 0,1 рад сила трения покоя увеличивается.
3) В случае, когда угол наклона плоскости составляет 0,1 рад, сила нормальной реакции больше 10 Н.
4) Коэффициент трения скольжения равен 0,5.
5) Брусок покоится, когда угол наклона плоскости составляет 0,6 рад.

ответ: 23

6)На поверхности воды плавает деревянный брусок. Как изменятся масса вытесненной воды и действующая на брусок сила Архимеда, если его заменить бруском той же плотности и той же массы, но меньшей высоты? Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменится

ответ: 33

7)Грузовик, движущийся по прямой горизонтальной дороге со скоростью υ, затормозил так, что колёса перестали вращаться. Масса грузовика m, коэффициент трения колёс о дорогу μ. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих движение грузовика. Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ответ: 32

8)При увеличении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул гелия увеличилась в 4 раза. Какова начальная температура газа?

ответ: 200

9)У идеального теплового двигателя Карно температура нагревателя 500 К, а температура холодильника 300 К. Определите КПД теплового двигателя.

ответ: 40

10)В закрытом сосуде под поршнем находится водяной пар при температуре 100 °С под давлением 20 кПа. Каким станет давление пара, если, сохраняя его температуру неизменной, объём пара уменьшить в 4 раза?

ответ: 80

11)Выберите из предложенного перечня два верных утверждения, которые сделать анализируя данный график: 1) Температура плавления первого тела в 1,5 раза больше, чем второго. 2) Тела имеют одинаковую удельную теплоёмкость в твёрдом агрегатном состоянии. 3) Удельная теплоёмкость второго тела в твёрдом агрегатном состоянии в 3 раза больше, чем первого. 4) Оба тела имеют одинаковую удельную теплоту плавления. 5) Тела имеют одинаковую удельную теплоёмкость в жидком агрегатном состоянии.

ответ: 35

12)При исследовании изопроцессов использовался закрытый сосуд переменного объёма, заполненный аргоном и соединённый с манометром. Объём сосуда медленно уменьшают, сохраняя температуру аргона в нём неизменной. Как изменяются при этом внутренняя энергия аргона в сосуде и его плотность? Для каждой величины определите соответствующий характер изменения:

1) увеличивается
2) уменьшается
3) не изменится

ответ: 31

13)Отрицательный заряд –q находится в поле двух неподвижных зарядов: положительного +Q и отрицательного –Q (см. рисунок). Куда направлено относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) ускорение заряда –q в этот момент времени, если на него действуют только заряды +Q и –Q?

ответ: вниз

14)Энергия магнитного поля катушки с током 0,64 Дж. Индуктивность катушки 20 мГн. Какова сила тока в катушке?

ответ: 8

15)Конденсатор, заряженный до разности потенциалов U, в первый раз подключили к катушке с индуктивностью L, а во второй – к катушке с индуктивностью 4L. Каково отношение периодов колебаний энергии конденсатора T2/T1 в этих двух случаях? Потерями энергии в контуре пренебречь.

ответ: 2

16)В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания. Из приведенного ниже списка выберите две величины, которые остаются постоянными при этих колебаниях. 1) Период колебаний силы тока в контуре; 2) Фаза колебаний напряжения на конденсаторе; 3) Заряд конденсатора; 4) Энергия магнитного поля катушки; 5) Амплитуда колебаний напряжения на катушке.

ответ: 15

17)Протон в однородном поле между полюсами магнита движется по окружности радиусом r с частотой обращения ν и центростремительным ускорением ацс. В этом же поле по окружности с таким же радиусом стала двигаться α-частица, обладающая такой же энергией, как и протон. Как изменились частота обращения в магнитном поле и центростремительное ускорение α-частицы по сравнению с протоном? Для каждой величины определите соответствующий характер её изменения:

1) увеличится
2) уменьшится
3) не изменится

ответ: 22

21)При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент поочерёдно освещался через различные светофильтры. В первой серии опытов использовался светофильтр, пропускающий только фиолетовый свет, а во второй – пропускающий только зелёный. В каждом опыте наблюдали явление фотоэффекта и измеряли запирающее напряжение. Как изменились частота падающей световой волны и запирающее напряжение при переходе от первой серии опытов ко второй? Для каждой величины определите соответствующий характер её изменения: 1) увеличится 2) уменьшится 3) не изменится

ответ: 22

22)На какую величину, согласно показаниям манометра, давление воздуха в баллоне превышает атмосферное давление, если погрешность манометра равна 3 мм рт. ст.?

ответ: 1963

23)Необходимо сделать нитяной маятник и с его помощью экспериментально определить ускорение свободного падения. Для этого школьник уже взял штатив с муфтой и лапкой, линейку и нить. Какие два предмета из приведенного ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента? 1) Секундомер 2) Динамометр 3) Мензурка 4) Электронные весы 5) Алюминиевый шарик

ответ: 15

24)Выберите все утверждения, которые соответствуют характеристикам звезд.

1) Температура α-Центавра А соответствует температуре звезд спектрального класса О.
2) Звезда Ригель является сверхгигантом.
3) Наше Солнце относится к гигантам спектрального класса В.
4) Средняя плотность звезды Сириус В больше, чем у Солнца.
5) Звезда Альдебаран не относится к звездам главной последовательности на диаграмме Герцшпрунга-Рессела.

ответ: 245

25)В калориметре находятся в тепловом равновесии 50 г воды и 5 г льда. Какой должна быть минимальная масса болта, имеющего удельную теплоёмкость 500 Дж/(кг ⋅К) и температуру 339 К, чтобы после опускания его в калориметр весь лёд растаял? Тепловыми потерями пренебречь.

ответ: 50

26)Пороговая чувствительность сетчатки человеческого глаза к видимому свету составляет 1,65∙10 –18 Вт, при этом на сетчатку глаза ежесекундно попадает 5 фотонов. Определите, какой длине волны это соответствует.

ответ: 600

27)Две плоские пластины конденсатора, закреплённые на изолирующих штативах, расположили на небольшом расстоянии друг от друга и соединили одну пластину с заземлённым корпусом, а другую со стержнем электрометра (см. рисунок). Затем пластину, соединённую со стержнем электрометра, зарядили. Объясните, опираясь на известные Вам законы, как изменяются показания электрометра при внесении между пластинами диэлектрической пластины. Отклонение стрелки электрометра пропорционально разности потенциалов между пластинами.

28)Нить, удерживающая вертикально расположенную легкую пружину в сжатом на 1 см состоянии, внезапно оборвалась (см. рисунок). Какова масса шарика, который приобретает начальную скорость 10 м/с? Жесткость пружины 2 кН/м. Колебаниями пружины после отрыва шарика пренебречь.

29)Два тела подвешены за нерастяжимую и невесомую нить к идеальному блоку, как показано на рисунке. При этом первое тело массой m1 = 500 г движется из состояния покоя вниз с ускорением а. Если первое тело опустить в воду с плотностью ρ = 1000 кг/м3 , находящемуся в большом объеме, система будет находиться в равновесии. При этом объем погруженной в воду части тела равен V = 1,5·10-4 м 3 . Сделайте рисунки с указанием сил, действующих на тела в обоих случаях. Определите ускорение а первого тела.

30)В вертикальном цилиндре с гладкими стенками, открытом сверху, под поршнем находится одноатомный идеальный газ. В начальном состоянии поршень массой M и площадью основания S покоится на высоте h, опираясь на выступы (см. рис. 1). Давление газа p0 равно внешнему атмосферному. Какое количество теплоты Q нужно сообщить газу при медленном его нагревании, чтобы поршень оказался на высоте H (см. рис. 2)? Тепловыми потерями пренебречь.

31)На рисунке показана схема электрической цепи, состоящей из источника тока с ЭДС Ɛ = 12 В и внутренним сопротивлением r = 1 Ом, двух резисторов с сопротивлениями R1 = 7 Ом и R2 = 4 Ом, конденсатора емкостью С = 3 мкФ и катушки с индуктивностью L = 32 мкГн. Какое количество теплоты выделится элементах цепи после размыкания ключа К? Сопротивлением провода катушки пренебречь.

32)На поверхности воды плавает надувной плот шириной 4 м и длиной 6 м. Небо затянуто сплошным облачным покровом, полностью рассеивающим солнечный свет. На какой максимальной глубине под плотом должна находиться маленькая рыбка, чтобы ее не увидели плавающие вокруг плота хищники? Глубиной погружения плота, рассеиванием света водой и его отражением от дна водоема пренебречь. Показатель преломления воды относительно воздуха принять равным 4/3.

Источник